Two recent papers provide useful techniques for “nowcasting” EM economies. The first uses “dynamic factor models” with high frequency indicators to estimate GDP growth in countries with scant and noisy data. The second uses seasonal adjustment with modifications for time-varying holidays that can track underlying trends in China and other countries with lunar year and Islamic holidays.
Luciani, Matteo, Madhavi Pundit, Arief Ramayandi, and Giovanni Veronese (2015). “Nowcasting Indonesia,” Finance and Economics Discussion Series 2015-100. Washington: Board of Governors of the Federal Reserve System
http://dx.doi.org/10.17016/FEDS.2015.100.
Roberts Ivan and Graham White (2015), “Seasonal Adjustment of Chinese Economic Statistics”, Reserve Bank of Australia, Research Discussion Paper, 2015-13
http://www.rba.gov.au/publications/rdp/2015/pdf/rdp2015-13.pdf
The below are excerpts from the paper. Headings and cursive text have been added.
Dynamic factor models
“GDP data provide the most comprehensive picture of the economy, by aggregating activity of different sectors. Unfortunately, the data come with long delays and are not available on a high frequency basis….High frequency data in emerging market economies are often scant, noisy, released with a lag, and can have missing information.”
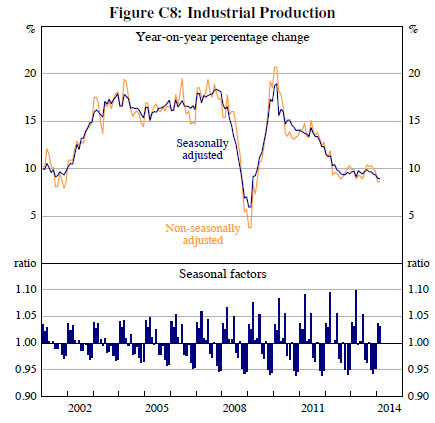
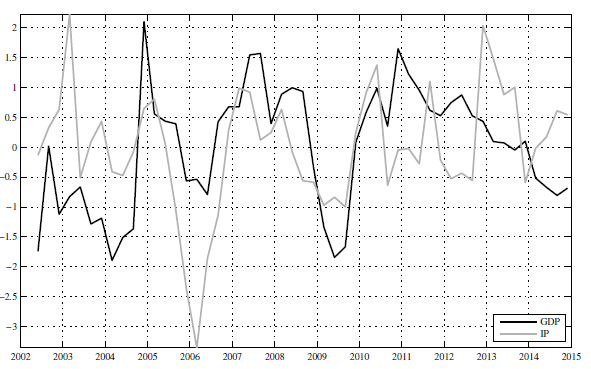
“Indonesia provides an interesting training case for developing a nowcasting framework that can be applied to monitor other similar economies [since data scarcity and quality problems are a particularly acute]…[For example]…a close examination on the relation between Indonesia’s GDP growth…industrial production [a popular high-frequency proxy elsewhere] shows that the two are only weakly linked.”
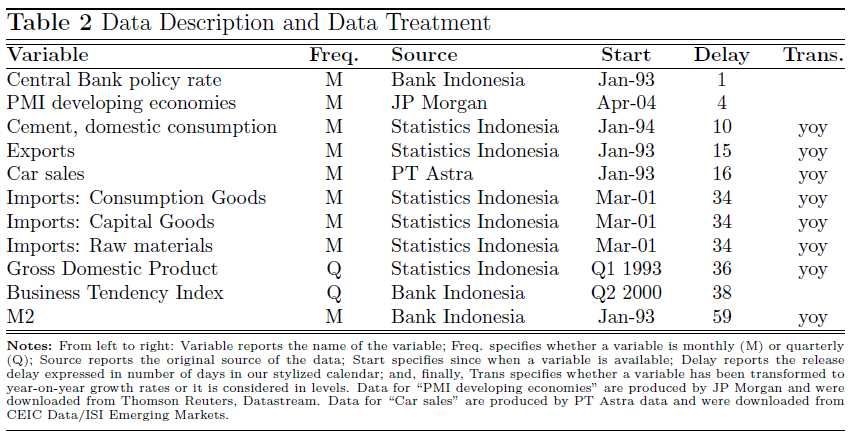
“We produce ‘predictions’ of the current state of the Indonesian economy by estimating a dynamic factor model on a dataset of eleven indicators (also followed closely by market operators) over the time period 2002 to 2014.”
“[A dynamic factor model]… is able to cope with missing data and mixed frequency indicators…[and] has become a standard tool for monitoring economic activity… Factor models are based on the idea that macroeconomic fluctuations are the result of few macroeconomic shocks, which affect the whole economy, and a number of sectoral/regional shocks that affect a part of the economy. Therefore, each variable in the dataset can be decomposed into a common part and an idiosyncratic part, where the common part is…meant to capture the co-movement in the data, i.e. the business cycle.”
“We…use the model to produce real-time predictions of Indonesian GDP growth… The model is estimated at the beginning of each quarter using only information available as of the first day of the quarter, and then the parameters are held fixed until the next quarter.”
“A possible strategy to draw from a large pool of variables could be to rely on a purely mechanical statistical selection procedure…[such as] selecting with the LARS [least-angle regression] algorithm only those variables that are really informative for forecasting the target variable.”
“An alternative strategy is to exploit the ‘revealed preferences’ of professional forecasters who follow the Indonesian economy on the Bloomberg platform…Since Bloomberg constantly ranks the analysts’ demand for these alerts by constructing a relevance index for each macroeconomic indicator, we can select variables based on this relevance index… For Indonesia only a relatively small number of macroeconomic series are tracked in real-time by the markets… strategy, we end up with a data set of ten macroeconomic indicators plus GDP.”
“Incorporating high frequency data in a rigorous framework leads to an improvement in the forecast accuracy of Indonesia’s economy compared to simple…benchmarks…Our model does well in predicting quarterly GDP growth when compared to private forecasters such as Bloomberg, and…when compared to institutional forecasts of the International Monetary Fund and the Asian Development Bank.”
Combined seasonal and holiday adjustment (China)
“The purpose of seasonal adjustment is to filter, or ‘look through’, the volatility resulting from the effects of seasonality in original data. Ideally, seasonal adjustment should clarify whether a movement in a given series is larger than would be expected, given knowledge of the regular seasonal pattern for that series…Until 2011… China’s National Bureau of Statistics did not publish seasonally adjusted data, and at present only a handful of series are available in this form.”
“Otherwise regular seasonal patterns in China are often clouded by calendar effects associated with traditional festivals, the timing of which is dictated by the lunar calendar and therefore varies from year to year on the Gregorian calendar….The Chinese New Year holiday receives international attention as the ‘world’s largest human migration’…[and] gives rise to noticeable variation in consumption and production patterns across the country…The timing of Chinese New Year on the Gregorian calendar fluctuates between 21 January and 20 February. This gives rise to distortions in simple computations for assessing the rate of change…such as year-on-year growth or inflation rates.”
“The X-12-ARIMA [seasonal adjustment based on an ‘autoregressive integrated moving average’ time series model] and SEATS [Signal Extraction in ARIMA Time Series]…can be used to adjust data affected by the Chinese New Year and other moving holidays. These procedures assume… the time series is a multiplicative combination of five unobserved components: trend, seasonal, trading day, holiday, and irregular. The trading day and holiday components represent calendar effects: trading day effects are related to the number of days and the number of working days in a month, while holiday effects are related to moving holidays…The irregular component is a residual that combines all fluctuations not covered by the other components in the decomposition”
“Both…procedures first implement a pre-adjustment stage which estimates corrections for Chinese New Year and/or other moving holidays. When the data have been…cleaned of outliers and deterministic calendar effects they are fed into a seasonal adjustment procedure that undertakes the decomposition of the cleaned series into trend, seasonal and irregular components….To account for the effect of moving holidays on Chinese data within the X-12-ARIMA and SEATS frameworks…a selection of dummy variables are used to purge the data of calendar effects. … Using an historical documentation of public holidays associated with Chinese New Year, we attempt to optimise the selection of these corrections prior to seasonal adjustment….Our procedure also extends existing approaches by explicitly taking into account the effects of the two main other, shorter lunar holidays, the Dragon Boat festival (duanwujie) in May/June and the Mid-Autumn festival (zhongqiujie) in September/October.”
“It is worth comparing these results to those of simpler approaches. One of the most widely reported methods…is to use the year-on-year percentage change… However, when a moving holiday is present there are typically very sharp movements in the year-on-year growth rate during the months in which the holiday can occur.”
“Analyses of data from other economies include…an application of X-12-ARIMA to 10 economic series in Taiwan…X-12-ARIMA and SEATS… seasonal adjustments of Korean time series in the presence of the traditional holidays such as Seollal (lunar New Year’s Day) and Chuseok (Korean Thanksgiving Day)…a similar approach to adjust Malaysian data in the presence of moving calendar effects arising from traditional holidays including Islamic observances such as Eid-ul Fitr and Eid-ul Adha, the Hindu festival of Deepavali and Chinese New Year.”